Question

Suppose f left parenthesis x right parenthesis right arrow 150f(x)→150 and g left parenthesis x right parenthesis right arrow 0g(x)→0 with ​g(x)less than<0 as x right arrow 3x→3. Determine modifyingbelow lim with x right arrow 3 startfraction f left parenthesis x right parenthesis over g left parenthesis x right parenthesis endfractionlimx→3 f(x) g(x).

Answer 1

`\lim_(x \to 3) ((f(x))/(g(x)) )=- \infty`

Explanation:

Given that:

f(x) approaches 150, and

g(x) approaches 0, with g(x) < 0,

as x approaches 3.

This means:

`\lim_(x \to 3) f(x)=150 \\\\ \lim_(x \to 3) g(x)=0`

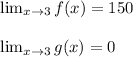
We need to evaluate:

`\lim_(x \to 3) ((f(x))/(g(x)) )`

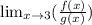
Distributing the limit to numerator and denominator, we get:

`( \lim_(x \to 0) f(x) )/( \lim_(x \to 0) g(x))\\\\ = (150)/(0)`

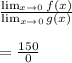
The expression will result in infinity as the answer, but since, g(x) < 0, this means g(x) is approaching 0 from the negative side. As a result, the expression 150/0 will approach negative infinity as x will approach 3.

Therefore, we can conclude:

`\lim_(x \to 3) ((f(x))/(g(x)) )=- \infty`