Answer:
The limit of this function does not exist.
Explanation:
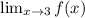

To find the limit of this function you always need to evaluate the one-sided limits. In mathematical language the limit exists if
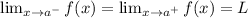
and the limit does not exist if
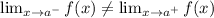
Evaluate the one-sided limits.
The left-hand limit
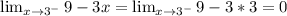
The right-hand limit
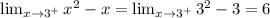
Because the limits are not the same the limit does not exist.