Answer:
1) Dimensions of shear rate is
![[T^(-1)]](https://img.qammunity.org/2020/formulas/engineering/college/ytrgzqr05vcb48ydl95m8bmx0zc857ij44.png) .
.
2)Dimensions of shear stress are
![[ML^(-1)T^(-2)]](https://img.qammunity.org/2020/formulas/engineering/college/qi7b4nzxglr1s1cwo8dnwa7zme7mvsnnle.png)
Step-by-step explanation:
Since the dimensions of velocity 'v' are
![[LT^(-1)]](https://img.qammunity.org/2020/formulas/engineering/college/89lyf4wk8flra1z4n6jmj4ilwnjjwor0eq.png) and the dimensions of distance 'y' are
and the dimensions of distance 'y' are
![[L]](https://img.qammunity.org/2020/formulas/physics/college/1dqrvvuikfamw6turse41aaa6za38s2dke.png) , thus the dimensions of
, thus the dimensions of
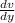 become
become
![([LT^(-1)])/([L])=[T^(-1)]](https://img.qammunity.org/2020/formulas/engineering/college/mcb9y5qiqscsyidbpassgpndf9oqb39yu4.png) and hence the units become
and hence the units become
 .
.
Now we know that the dimensions of coefficient of dynamic viscosity
 are
are
![[ML^(-1)T^(-1)]](https://img.qammunity.org/2020/formulas/engineering/college/dd8xebt67ph6pq3kvqz1aioh9uqdtan5wn.png) thus the dimensions of shear stress can be obtained from the given formula as
thus the dimensions of shear stress can be obtained from the given formula as
![[\tau ]=[ML^(-1)T^(-1)]* [T^(-1)]\\\\[\tau ]=[ML^(-1)T^(-2)]](https://img.qammunity.org/2020/formulas/engineering/college/ukgxy7igfvjknwdajdpf26o674mh759lgh.png)
Now we know that dimensions of momentum are
![[MLT^(-1)]](https://img.qammunity.org/2020/formulas/engineering/college/b124qho5zq4premxg2qc7wrf5uwz5mlgkd.png)
The dimensions of
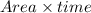 are
are
![[L^(2)T]](https://img.qammunity.org/2020/formulas/engineering/college/cwt45iinl3fv11wazj2xdf9u2ah2zliczi.png)
Thus the dimensions of
![(Moumentum)/(Area* time)=(MLT^(-1))/(L^(2)T)=[MLT^(-2)]](https://img.qammunity.org/2020/formulas/engineering/college/jv1raohuvr4dyrpc5q8oy48az7tc9n6vbe.png)
Which is same as that of shear stress. Hence proved.