Question

What sine function represents an amplitude of 4, a period of pi over 2, no horizontal shift, and a vertical shift of −3?

f(x) = −3 sin 4x + 4

f(x) = 4 sin 4x − 3

f(x) = 4 sin pi over 2x − 3

f(x) = −3 sin pi over 2x + 4

Answer 1

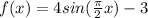`f(x) = 4sin((\pi)/(2)x) - 3`, the third one

Explanation:

Explaining the sine function:

The sine function is defined by:

`S = Asin(p(x - x_(0))) + V`

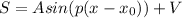
In which A is the amplitude,
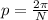`p = (2\pi)/(N)` is the period,
`x_(0)` is the horizontal shift and V is the vertical shift.

So, in your problem:

The amplitude is 4, so A = 4.

The period is
`(\pi)/(2)`, so
`p = (\pi)/(2)`.

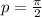There is no horizontal shift, so
`x_(0) = 0`.

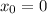The vertical shift is −3, so V = -3.

The sine function that represents these following conditions is

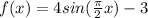`f(x) = 4sin((\pi)/(2)x) - 3`, the third one