Answer:
Last option: It is not a function because there are two different y-values for a single x-value.
Explanation:
It is necessary to remember that, by definition, a relation is a function if each input value (x-value) has one and only one output value (x-value) .
In this case, the following points:
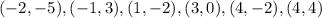
You can observe that the input value 4 (
 ) has two ouput values. These are:
) has two ouput values. These are:
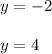
Therefore, since there are two different y-values for a single x-value, you can conclude that the given graph is not a function.