Answer:
The possible dimensions of the region are
52 ft by 16 ft
32 ft by 26 ft
Explanation:
Let
x -----> the length of the rectangular region
y ----> the width of the rectangular region
we know that
The perimeter of a rectangle is equal to
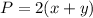
Remember that
A kennel owner wants to subdivide this region into three smaller rectangles of equal length
so
we also have to take into account the divisions
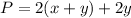
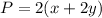
we have


simplify
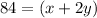 ----->
----->
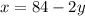 -----> equation A
-----> equation A
The total area to be enclosed is 832 ft^2
The area is equal to
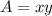
so
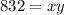 ----> equation B
----> equation B
substitute equation A in equation B
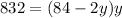
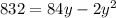
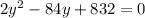
Solve the quadratic equation by graphing
The solution are y1=16 ft, y2=26 ft
see the attached figure
For
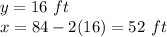
For

therefore
The possible dimensions of the region are
52 ft by 16 ft
32 ft by 26 ft