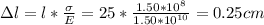Question

Assume Young’s modulus for bone is 1.50 3 1010 N/m2. The bone breaks if stress greater than 1.50 3 108 N/m2 is imposed on it. (a) What is the maximum force that can be exerted on the femur bone in the leg if it has a minimum effective diameter of 2.50 cm? (b) If this much force is applied compressively, by how much does the 25.0-cm-long bone shorten?

Answer 1

`F_(max)=2.95*10^(5)N`

`\Delta l=0.25cm`

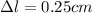
Step-by-step explanation:

E=1.50x10^10 N/m2 Young's modulus of bone

σmax=1.50x10^8 N/m2 Max stress tolerated by the bone

Relation between stress and Force:

`\sigma=(F)/(A)=(F)/(\pi*d^(2)/4)`

`F_(max)=\sigma_(max)*\pi*d^(2)/4}=1.50*10^(8)*\pi*(2.5*10^(-2))^(2)=2.95*10^(5)N`

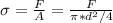
Relation between stress and strain:

Young's modulus is defined by the ratio of longitudinal stress σ , to the longitudinal strain ε:

`E=(\sigma)/(\epsilon)`

`\epsilon=(\Delta l)/(l)`

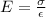
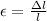
We solve these equations to find the bone compression:

`\Delta l=l*(\sigma)/(E)=25*(1.50*10^(8))/(1.50*10^(10))=0.25cm`