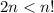Question

Prove using the principle of mathematical induction: (i) The number of diagonals of a convex polygon with n vertices is n(n − 3)/2, for n ≥ 4, (ii) 2n < n! for for all n > k > 0, discover the value of k before doing induction.

Answer 1

Explanation:

Proof for i)

We will prove by mathematical induction that, for every natural
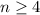`n\geq 4`, the number of diagonals of a convex polygon with n vertices is
`(n(n-3))/(2)`.

In this proof we will use the expression d(n) to denote the number of diagonals of a convex polygon with n vertices

Base case:

First, observe that:, for n=4, the number of diagonals is

`2=(n(n-3))/(2)`

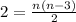
Inductive hypothesis:

Given a natural
`n \geq 4`,

`d(n)=(n(n-3))/(2)`

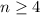Now, we will assume the induction hypothesis and then use this assumption, involving n, to prove the statement for n + 1.

Inductive step:

Observe that, given a convex polygon with n vertices, wich we will denote by P(n), if we add a new vertix (transforming P(n) into a convex polygon with n+1 vertices, wich we will denote by P(n+1)) we have that:

• Every diagonal in P(n) will still be a diagonal in P(n+1).
• One (and only one) side of P(n) will be a diagonal in P(n+1).
• There would be an extra n-2 diagonals (those that connect with the new added vertix).

Because of these observation we know that, for every
`n\geq 4`,

`d(n+1)=d(n)+1+(n-2)=d(n)+n-1`

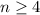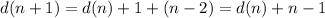
Therefore:

`d(n+1)=d(n)+n-1=(n(n-3))/(2)+n-1=(n^2-3n+2n-2)/(2)=(n^2-n-2)/(2)=((n+1)(n-2))/(2)`

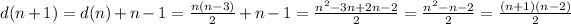
With this we have proved our statement to be true for n+1.

In conlusion, for every natural
`n \geq 4`,

`d(n)=(n(n-3))/(2)`

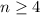Proof for ii)

Observe that:

• For n=1
  `2n=2>1=n!`
• For n=2
  `2n=4>2=n!`
• For n=3
  `2n=6=n!`

Then, the statement is not true for n=1,2,3.

We will prove by mathematical induction that, for every natural
`n \geq 4`,

`2n<n!`.

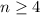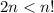Base case:

For n=4,
`2n=8<24=n!`

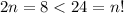
Inductive hypothesis:

Given a natural
`n \geq 4`,
`2n<n!`

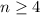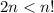
Now, we will assume the induction hypothesis and then use this assumption, involving n, to prove the statement for n + 1.

Inductive step:

Observe that,

`n!+2\leq (n+1)! \iff n!+2\leq n!(n+1) \iff 1+(2)/(n!)\leq n+1 \iff 2\leq n*n!`

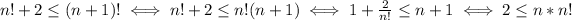
wich is true as we are assuming
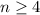`n\geq 4`. Therefore:

`2(n+1)=2n+2<n!+2\leq (n+1)!`

With this we have proved our statement to be true for n+1.

In conlusion, for every natural
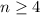`n \geq 4`,

`2n<n!`