Question

At a large department store, the average number of years of employment for a cashier is 5.7 with a standard deviation of 1.8 years. If the number of years of employment at this department store is normally distributed, what is the probability that a cashier selected at random has worked at the store for over 10 years?

Answer 1

Answer: 0.0019

Explanation:

Let x be the random variable that represents the number of years of employment at this department store.

Given : The number of years of employment at this department store is normally distributed,

Population mean :
`\mu=5.7`

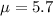
Standard deviation :
`\sigma=1.8`

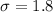
Z-score :
`z=(x-\mu)/(\sigma)`

Now, the z-value corresponding to 10 :
`z=(10-5.7)/(1.8)\approx2.39`

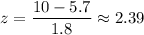
P-value =
`P(x>10)=P(Z>2.89)=1-P(z\leq2.89)`

`=1-0.9980737=0.0019263\approx0.0019\text{ (Rounded to nearest ten thousandth)}`

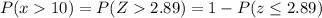
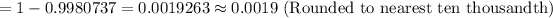
Hence, the probability that a cashier selected at random has worked at the store for over 10 years = 0.0019