Question

Find a parametric equation for the line through the point ( - 5, - 6, - 6) and perpendicular to the plane 2x + 3y + 9z = 17 which is written using the coordinates of the given point and the coefficients of x, y, and z in the given equation of the plane. Type expressions using t as the variable.)

Answer 1

x=-5+2t, y=-6+3t, z=-6+9t

Explanation:

We need to find parametric equations for the line through the point ( - 5, - 6, - 6) and perpendicular to the plane 2x + 3y + 9z = 17 .

If a line passes through a point
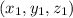`(x_1,y_1,z_1)` and perpendicular to the plane
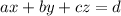`ax+by+cz=d`, then the Cartesian form of line is

`(x-x_1)/(a)=(y-y_1)/(b)=(z-z_1)/(c)`

and parametric equations are

`x=x_1+at,y=y_1+bt,z=z_1+ct`

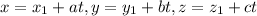
For the given information,
`x_1=-5,y_1=-6,z_1=-6,a=2,b=3,c=9`. So, the Cartesian form of line is

`(x+5)/(2)=(y+6)/(3)=(z+6)/(9)`

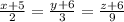
Parametric equations of the line are

`x=-5+2t`

`y=-6+3t`

`z=-6+9t`

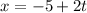
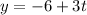
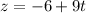
Therefore the parametric equation for the line are x=-5+2t, y=-6+3t, z=-6+9t.