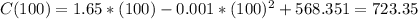Question

A company estimates that the marginal cost (in dollars per item) of producing x items is 1.65 − 0.002x. If the cost of producing one item is $570, find the cost of producing 100 items. (Round your answer to two decimal places.)

Answer 1

The cost of producing 100 items is $723.35

Explanation:

The marginal cost is the derivative of the total cost function, so we have

`C^(')(x)=1.65-0.002x`

To find the total cost function we need to do integration

`C(x)= \int\, C^(')(x)dx \\C(x)=\int\,(1.65-0.002x) dx`

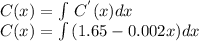
Apply the sum rule to find the integral

`\int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)`

`\int \:1.65dx=1.65x\\\int \:0.002xdx=0.001x^2`

`C(x)=\int\,(1.65-0.002x) dx = 1.65x-0.001x^2+D`

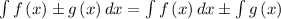
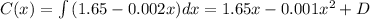
D is the constant of integration

We are given that C(1) = $570, we can use this to find the value of the constant in the total cost function

`C(1)=570=1.65*(1)+0.001*(1)^2+D\\D=570-1.649=568.351`

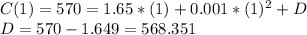
So the total cost function is
`C(x)=1.65x-0.001x^2+568.351` and the cost of producing 100 items is

x=100

`C(100)=1.65*(100)-0.001*(100)^2+568.351 = 723.35`