Step-by-step explanation:
Let us take the volume of block is x.
Since, the block is floating this means that it is in equilibrium. Formula to calculate net force will be as follows.
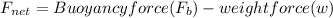
Also, buoyancy force
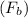 = (volume submerged in water × density of water) + (volume in oil × density of oil)
= (volume submerged in water × density of water) + (volume in oil × density of oil)
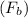 =
=

=
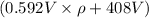 g
g
As, W = V × density of graphite × g
It is given that density of graphite is
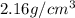 or 2160
or 2160
 .
.
So, W = 2160 V g
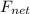 = (0.592 V \rho + 408 V) g - 2160 V g = 0
= (0.592 V \rho + 408 V) g - 2160 V g = 0
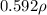 = 1752
= 1752
 = 2959.46
= 2959.46
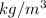 or 2.959
or 2.959
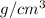 is the density of oil.
is the density of oil.
It is given that mass of flask is 124.8 g.
Mass of 35.3
 oil =
oil =
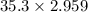 104.7 g
104.7 g
Hence, in second weighing total mass will be calculated as follows.
(124.8 + 104.7) g
= 229.27 g
Thus, we can conclude that in the second weighing mass is 229.27 g.