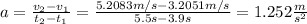Answer:
a)
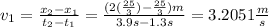
b)
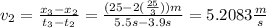
c)
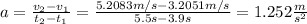
Step-by-step explanation:
The knowable variables are
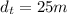
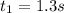
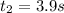
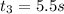
Since the three traffic signs are equally spaced, the distance between each sign is
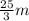
a)
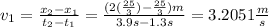
b)
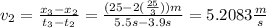
Since we know the velocity in two points and the time the car takes to pass the traffic signs
c)