Question

A teacher sends her students on a treasure hunt. She gives the following instructions: · Walk 300 m north · Walk 400 m northwest · Walk 700 m east-southeast and the treasure is buried there. As all the other students walk off following the instructions, Jane physics student quickly adds the displacements and walks in a straight line to find the treasure. How far (in meters) does Jane need to walk?

Answer 1

Magnitude of displacement = 481.24 m

Direction = 40.88 degrees north east.

Step-by-step explanation:

Let east is along real axis and north is along imaginary axis. So,

First walk = d1 = J300 m

Second walk = d2 = -400Cos(45) + J400Sin(45) = (-282.84 + J282.84) m

Third walk = d3 = 700Cos(22.5) – J700Sin(22.5) = (646.71 – J267.88) m

Total displacement = d = d1 + d2 + d2 = (363.86 + J314.96)m

Magnitude = √((363.86)^2+(314.96)^2) = 481.24 m

Direction = arctan(314.96/363.86) = 40.88 degrees north east.

Answer 2

displacement is 481.3 m with 40.88° north east

Step-by-step explanation:

given data

walk 1 = 300 m north = 300 j

walk 2 = 400 m northwest =400 cos(45) i + sin(45) j

walk 3 = 700 m east southeast = 700 cos(22.5) i- sin(22.5) j

to find out

displacement and direction

solution

we consider here direction x as east and direction y as north

so

displacement = distance 1 + distance 2 + distance 3

displacement = 300 j + 400 cos(45) i + sin(45) j + 700 cos(22.5) i- sin(22.5) j

we get here

displacement = 363.9 i + 315 j

so magnitude

displacement =
`\sqrt{363.9^(2)+315^(2)  }`

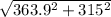
displacement = 481.3 m

and angle will be = arctan(315/369.9)

angle = 0.713494059 rad

angle is 40.88 degree

so displacement is 481.3 m with 40.88° north east