Answer:
There is a 44.12% probability that the defective product came from C.
Explanation:
This can be formulated as the following problem:
What is the probability of B happening, knowing that A has happened.
It can be calculated by the following formula
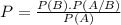
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
-In your problem, we have:
P(A) is the probability of the customer receiving a defective product. For this probability, we have:
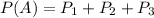
In which
 is the probability that the defective product was chosen from plant A(we have to consider the probability of plant A being chosen). So:
is the probability that the defective product was chosen from plant A(we have to consider the probability of plant A being chosen). So:
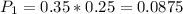
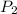 is the probability that the defective product was chosen from plant B(we have to consider the probability of plant B being chosen). So:
is the probability that the defective product was chosen from plant B(we have to consider the probability of plant B being chosen). So:
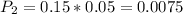
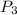 is the probability that the defective product was chosen from plant B(we have to consider the probability of plant B being chosen). So:
is the probability that the defective product was chosen from plant B(we have to consider the probability of plant B being chosen). So:

So
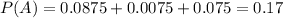
P(B) is the probability the product chosen being C, that is 50% = 0.5.
P(A/B) is the probability of the product being defective, knowing that the plant chosen was C. So P(A/B) = 0.15.
So, the probability that the defective piece came from C is:
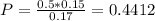
There is a 44.12% probability that the defective product came from C.