Answer:
The T-score is 2.49216
Explanation:
A 98% confidence interval should be estimated for the end times of cyclists. Since the sample is small, a T-student distribution should be used, in such an estimate. The confidence interval is given by the expression:
![[\bar x -T_{(n-1,(\alpha)/(2))} (S)/(√(n)), \bar x +T_{(n-1,(\alpha)/(2))} (S)/(√(n))]](https://img.qammunity.org/2020/formulas/mathematics/college/5yo5b8pey2r7pj0v58cadnvd1xda01aplk.png)
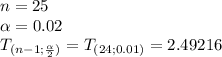
Then the T-score is 2.49216