Question

You plan to purchase an $110,000 house using a 15-year mortgage obtained from your local bank. The mortgage rate offered to you is 5.5 percent. You will make a down payment of 10 percent of the purchase price. a. Calculate your monthly payments on this mortgage. b. Calculate the amount of interest and, separately, principal paid in the 100th payment. c. Calculate the amount of interest and, separately, principal paid in the 130th payment. d. Calculate the amount of interest paid over the life of this mortgage.

Answer 1

Cuota: 808.91

100th cuota:

Amortization 561.07

Interest 247.84

130th cuota:

Amortization 561.07

Interest 247.84

Total Inerest:

$ 46,603.80

Step-by-step explanation:

We will first calculate the mortgage payment. which is the PTM of the present value of an ordinary annuity

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

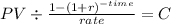
PV $99,000.00 (110,000 - 10% down payment)

time 180 (15 years x 12 month per year)

rate 0.004583333 (0.055 divided by 12 month per year

`99,000 * (1-(1+0.0045833)^(-180) )/(0.0045833) = C\\`

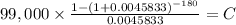
C $ 808.91

Now we will calculate "t" which is the amortization ofthe first period:

Cuota - Interest = t

interest: 99,000 x 0.00548333 = 453.75

808.91 - 453.75 = 355.16

Now will calculatize this by 100 period

and by 130 period to get the amortization in each k period.

`t\: (1+ r)^(k) = Amortization_k`

t = 355.16

k = 100

rate 0.00458

`355.16 \: (1+ 0.0045833)^(100) = Amortization_(100)`

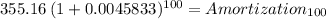
Amortization 561.07

For interest we subtract from the cuota:

808.91 - 561.07 = 247.84

We repeat for the 130th payment:

`355.16 \: (1+ 0.00458333333333333)^(130) = Amortization_(130)`

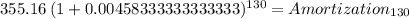
Amortization 643.58

808.91 - 561.07 = 247.84 interest

Total Interest:

Cuota x total payment - principal

808.91 x 180 - 99,000 = $ 46,603.80