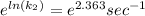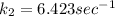Answer:
The rate constant
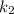 at 84.8°C is
at 84.8°C is
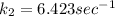
Step-by-step explanation:
Taking the Arrhenius equation we have:
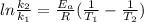
Where
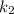 is the rate constant at a temperature 2,
is the rate constant at a temperature 2,
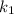 is the rate constant at a temperature 1;
is the rate constant at a temperature 1;
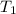 is the temperature 1,
is the temperature 1,
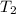 is the temperature 2, R is the gas constant and
is the temperature 2, R is the gas constant and
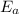 is the activation energy.
is the activation energy.
Now, we need to solve the equation for
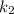 , so we have:
, so we have:
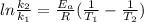
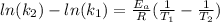
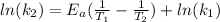
Then we need to make sure that we are working with the same units, so:
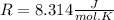
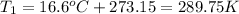
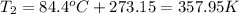
And now we can replace the values into the equation:
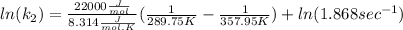
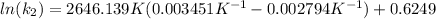
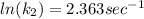
To solve the ln we have to apply e in both sides of the equation, so we have: