Answer: 40000
Explanation:
The formula to find the sample size is given by :-
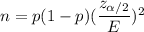 , where p is the prior estimate of the population proportion.
, where p is the prior estimate of the population proportion.
Here we can see that the sample size is inversely proportion withe square of margin of error.
i.e.
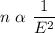
By the equation inverse variation, we have
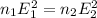
Given :
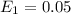
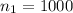

Then, we have
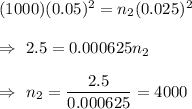
Hence, the sample size will now have to be 4000.