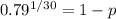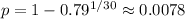Question

An aircraft seam requires 30 rivets. The seam will have to be reworked if any of these rivets is defective. Suppose rivets are defective independently of one another, each with the same probability. (Round your answers to four decimal places.) (a) If 21% of all seams need reworking, what is the probability that a rivet is defective?

Answer 1

`0.0078`

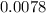
Explanation:

To compute the probability of a rivet being defective we can do the following:

The seam won't need reworking if the 30 rivets are working as intended. Since there's a 21% chance of the seam needing reworking, we then know that there's a 79% chance of the seam not needing reworking, which means that there's a 79% chance of having the 30 rivets working as intended. Now, each rivet is either defective with a probability p, or NOT defective with a probability 1-p. Since rivets are defective independently from one another, the probability of the 30 rivets working as intended is
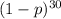`(1-p)^(30)`, and since we know this has a chance of happening of 79%, we get the equation:

`0.79=(1-p)^(30)`

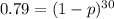
Solving for p, we get:

`0.79^(1/30)=1-p`

`p=1-0.79^(1/30)\approx 0.0078`