Question

A snowboarder starts from rest at the top of a double black diamond hill. As he rides down the slope, GPS coordinates are used to determine his displacement as a function of time, x = 0.5t3 + t2 + 2t, where x and t are expressed in feet and seconds, respectively. Determine the position, velocity, and acceleration of the boarder expressed when t = 12 seconds. (Round the final answer to one decimal place.)

Answer 1

`x(12s)=1032 feet\\v(12s)=242 feet/s\\a(12s)=38 feet/s^(2)`

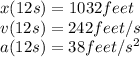
Step-by-step explanation:

Howdy!

To solve this question we need to know that the velocity v and acceleration a are the first and second derivatives of the position x respect to the time t.

Let's calculate these derivatives:

`v=(dx)/(dt)=0.5(d)/(dt)(t^(3) )+(d)/(dt)(t^(2))+(d)/(dt)(2t)`

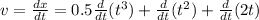
If we use the following formula:

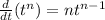`(d)/(dt)(t^(n) )=n t^(n-1)` --- (1)

we get that:

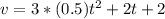`v = 3*(0.5)t^(2) + 2t+2` --- (2)

Now the acceleration:

`a=(d^(2)x)/(dt^(2))=(dv)/(dt)=1.5(d)/(dt)(t^(2) )+(d)/(dt)(2t})+(d)/(dt)(2)`

Therefore:

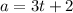`a=3t+2` --- (3)

To determine the position, velocity and acceleration at t=12 we must evaluate these functions at t=12:

`x(12) = 0.5*12^(3)+12^(2)+2*12\\v(12) = 1.5*12^(2)+2*12+2\\a(12)= 3*12+2`

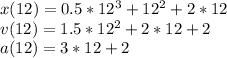
Evaluating these equations we obtain the required values:

`x(12s)=1032 feet\\v(12s)=242 feet/s\\a(12s)=38 feet/s^(2)`

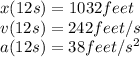
Greetings!