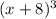Answer:
The inverse function of
![\sqrt{3]{x} - 8](https://img.qammunity.org/2020/formulas/mathematics/college/hpaaqrty02ubqxa93fyqvik1rprtlq9u01.png) is
is
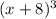
Explanation:
Inverse of a function:
To find the inverse of a function
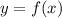 , basically, we have to reverse r. We exchange y and x in their positions, and then we have to isolate y.
, basically, we have to reverse r. We exchange y and x in their positions, and then we have to isolate y.
In your exercise:
![y = \sqrt[3]{x} - 8](https://img.qammunity.org/2020/formulas/mathematics/college/akjqwdzb3vq67oapx34rnpdz9glz6usml8.png)
Exchanging x and y, we have:
![x = \sqrt[3]{y} - 8](https://img.qammunity.org/2020/formulas/mathematics/college/5juc6dqp3vf435xgzm896ptojlej1b569y.png)
![x + 8 = \sqrt[3]{y}](https://img.qammunity.org/2020/formulas/mathematics/college/emi5idaq93u5erpmp7sh2u78ao3xevcf99.png)
Now we have to write y in function of x
![(x+8)^(3) = (\sqrt[3]{y})^(3)](https://img.qammunity.org/2020/formulas/mathematics/college/qvclr8lnibnk0qi1difk5nan3p3iizvqta.png)
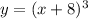
So, the inverse function of
![\sqrt{3]{x} - 8](https://img.qammunity.org/2020/formulas/mathematics/college/hpaaqrty02ubqxa93fyqvik1rprtlq9u01.png) is
is