Answer:
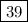
Explanation:

Let x = Total campers
and y = Archery sign up
In a direct proportionality,
y = kx
1. Calculate the value of k
Substitute a pair of values for x and y
150 = k × 45
Divide each side by 45
k = 150/45 = 10/3
2. Calculate the value of x in Week 3
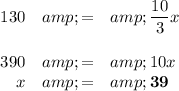
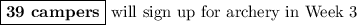
The diagram is a graph of your proportionality. It shows that y = 130 when x = 39.