Answer:
For the values of y greater than
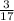
Explanation:
Suppose 5y-1 greater than the value of the fraction
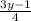
That is,
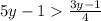
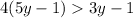
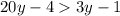
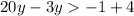
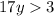
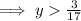 ( a > b ⇒
( a > b ⇒
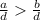 where, d > 0 )
where, d > 0 )
Hence, for the values of y greater than
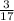 the value of the binomial 5y-1 greater than the value of the fraction
the value of the binomial 5y-1 greater than the value of the fraction
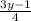 .
.