Answer:
(a) 0.9838 (b) 0.6553 (c) 13.05198
Explanation:
We have that the daily viewing time is a random variable normally distributed with mean and standard deviation
 = 8.35 hours and
= 8.35 hours and
 = 2.5 hours
= 2.5 hours
respectively. If we call the random variable X, the density function of this random variable is given by
f(x) =
![(1)/(√(2\pi)2.5)\exp[-((x-8.35)^(2))/(2(2.5)^(2))]](https://img.qammunity.org/2020/formulas/mathematics/college/82tmn5az8haupck0daczy64nlfnem2qw3m.png) , and we can calculate the next probabilities using a computer or a table from a book.
, and we can calculate the next probabilities using a computer or a table from a book.
(a) P(X>3)=
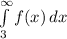 =0.9838
=0.9838
in the R statistical programming language we use the instruction pnorm(3, mean = 8.35, sd = 2.5, lower.tail = FALSE)
(b) P(
 ) =
) =
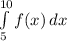 = 0.6553
= 0.6553
in the R statistical programming language we use the instruction
pnorm(10, mean = 8.35, sd = 2.5) - pnorm(5, mean = 8.35, sd = 2.5)
(c) You should find a value
 such that
such that
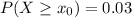 , this value is
, this value is
 =13.05198
=13.05198
The instruction qnorm(0.03, mean = 8.35, sd = 2.5, lower.tail = FALSE) give us 13.05198 in the R statistical programming language.