Answer: 10
Explanation:
The formula to find the sample size is given by :-
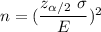
Given : Significance level :
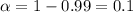
Critical z-value=
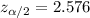
Margin of error : E=5
Standard deviation :
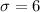
Now, the required sample size will be :_
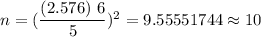
Hence, the final sample required to be of 10 .