Answer:
Yes, it is right-angled
Step-by-step explanation:
Two vectors are orthogonal if the scalar product between them is zero. Then, we will match each pair of vertices with a vector, wich is formed with the following formula:
Given two points A and B, the vector going from A to B is
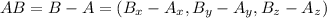
So, we calculate each component separately.
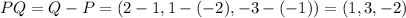

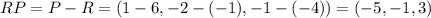
Finally, using the scalar product formula
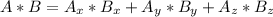
we see if the products is zero

In this case we don't even have to calculate the other products as we've found that PQ and QR form a right angle.