Question

An individual is now 50 years old, that he plans to retire in 10 years, and that he expects to live for 25 years after he retires, that is, until he is 85. He wants a fixed annual retirement income of $65,156. His retirement income will begin the day he retires, 10 years from today, and he will then get 24 additional annual payments. He currently has $100,000 saved up; and he expects to earn a return on his savings of 8 percent per year, annual compounding. To the nearest dollar, how much must he save during each of the next 10 years (with deposits being made at the end of each year) to meet his retirement goal?

Answer 1

Ans. He must save during each of the following 10 years, at the end of each year $32,452.

Step-by-step explanation:

Hi, in order to find the amount of money that he should have in ten years so he can receive an annual payment of $65,156 for 25 more years (24 payments), we need to bring to present value all 24 payments to year 10. Let me show you the formula.

`PresentValue_(10) =(A((1+r)^(n)-1) )/(r(1+r)^(n) )`

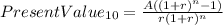
Where:

A= $65,156

n= 24

r= 0.08

Therefore the present value in year 10 is:

`PresentValue_(10) =(65,156((1+0.08)^(24)-1) )/(0.08(1+0.08)^(24) )=686,012`

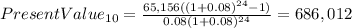
So that is our present value in year 10, or to put it in other words, our future value (if we look at it from year 0). Now we need to find the annuity (amount to save) that with account for $686,012, plus that $100,000 that he already has saved.

Every should look like this.

`686,012=100,000*(1+0.08)^(10) +(A((1+0.08)^(10)-1) )/(0.08(1+0.08)^(10) )`

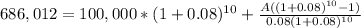
And we solve this equation for "A".

`686,012=A(14.4865625)+215,892`

`A=((686,012-215,892))/(14.4865625) =32,452`

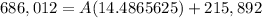
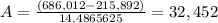
Best of luck.