Question

Calculate the kinetic energy in units of electron volts for an electron emitted from a surface with a work function of 1.5 eV that has been illuminated with632.8-nm (red) helium neon laser, such as those used in a supermarket scanner. Perform the same calculation for a 543.5-nm (green) helium-neon laser.

Answer 1

The kinetic energies are 0.46 eV and 0.78 eV.

Step-by-step explanation:

Given that,

Work function = 1.5 eV

Wavelength = 632.8 nm

We need to calculate the energy for red helium neon laser

Using formula of energy

`E=(hc)/(\lambda)`

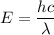
Put the value into the formula

`E=(4.136*10^(-15)*3*10^(8))/(632.8*10^(-9))`

`E=1.96\ eV`

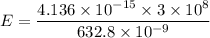
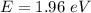
We need to calculate the kinetic energy

Using formula of K.E

`K.E=E-\phi`

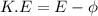
`\phi`=work function

E = energy

Put the value into the formula

`K.E=1.96-1.5`

`K.E=0.46\ eV`

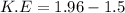
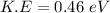
We need to calculate the energy for green helium neon laser

Using formula of energy

`E=(4.136*10^(-15)*3*10^(8))/(543.5*10^(-9))`

`E=2.28\ eV`

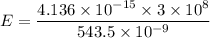
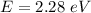
We need to calculate the kinetic energy

Using formula of K.E

`K.E=2.28-1.5`

`K.E=0.78\ eV`

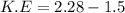
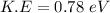
Hence, The kinetic energies are 0.46 eV and 0.78 eV.