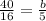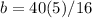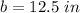Answer:
The sides of the first quadrilateral are 60 in, 40 in, 30 in and 12,5 in
The sides of the second quadrilateral are 24 in, 16 in, 12 in and 5 in
Explanation:
we know that
If two figures are similar, then the ratio of its corresponding sides is proportional, and this ratio is called the scale factor
Arrange the sides of each quadrilateral from largest to smallest
First quadrilateral Second quadrilateral
Longest side=60 in Longest side=c in
Second side=40 in Second side=16 in
Third side= a in Third side= 12 in
Fourth side=b in Fourth side=5 in
so
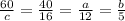
Find the value of c
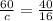

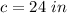
Find the value of a

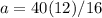
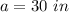
Find the value of b