Answers:
a)
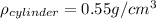
b)

c) When we divided both volumes (sumerged and displaced) the factor
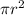 is removed during calculations.
is removed during calculations.
Step-by-step explanation:
a) According to Archimedes’ Principle:
A body totally or partially immersed in a fluid at rest, experiences a vertical upward thrust equal to the mass weight of the body volume that is displaced.
In this case we have a wooden cylinder floating (partially immersed) in water. This object does not completely fall to the bottom because the net force acting on it is zero, this means it is in equilibrium. This is due to Newton’s first law of motion, that estates if a body is in equilibrium the sum of all the forces acting on it is equal to zero.
Hence:
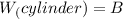 (1)
(1)
Where:
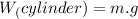 is the weight of the wooden cylinder, where
is the weight of the wooden cylinder, where
 is its mass and
is its mass and
 gravity.
gravity.
 is the Buoyant force, which is the force the fluid (water in this situation) exert in the submerged cylinder, and is directed upwards.
is the Buoyant force, which is the force the fluid (water in this situation) exert in the submerged cylinder, and is directed upwards.
We can rewrite (1) as follows:
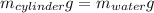 (2)
(2)
On the other hand, we know density
 establishes a relationship between the mass of a body andthe volume it occupies. Mathematically is expressed as:
establishes a relationship between the mass of a body andthe volume it occupies. Mathematically is expressed as:
 (3)
(3)
isolating the mass:
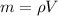 (4)
(4)
Now we can express (2) in terms of the density and the volume of cylinder and water:
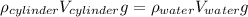 (5)
(5)
In this case
 is the volume of water displaced by the wooden cylinder (remembering Archimedes's Principle).
is the volume of water displaced by the wooden cylinder (remembering Archimedes's Principle).
At this point we have to establish the total volume of the cylinder and the volume of water displaced by the sumerged part:
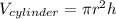 (6)
(6)
Where
 is the radius and
is the radius and
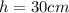 the total height of the cylinder.
the total height of the cylinder.
 (7)
(7)
Where
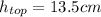 is the height of the top of the cylinder above the surface of water and
is the height of the top of the cylinder above the surface of water and
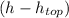 is the height of the sumerged part of the cylinder.
is the height of the sumerged part of the cylinder.
Substituting (6) and (7) in (5):
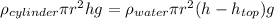 (8)
(8)
Clearing
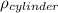 :
:
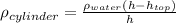 (9)
(9)
Simplifying;
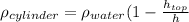 (10)
(10)
Knowing
 :
:
 (11)
(11)
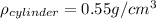 (12) This is the density of the wooden cylinder
(12) This is the density of the wooden cylinder
b) Now we have a different situation, we have the same wooden cylinder, which density was already calculated (
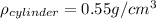 ), but the density of the liquid
), but the density of the liquid
 is unknown.
is unknown.
Applying again the Archimedes principle:
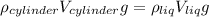 (13)
(13)
Isolating
 :
:
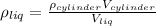 (14)
(14)
Where:
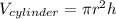
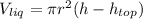
Then:
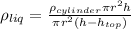 (15)
(15)
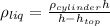 (16)
(16)
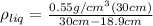 (17)
(17)
 (18) This is the density of the liquid
(18) This is the density of the liquid
c) As we can see, it was not necessary to know the radius of the cylinder (we did not need to knoe its length and width), we only needed to know the part that was sumerged and the part that was above the surface of the liquid.
This is because in this case, when we divided both volumes (sumerged and displaced) the factor
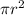 is removed during calculations.
is removed during calculations.