Question

The acceleration of a particle moving along a straight line is given by a = −kt2 m/s2 where k is a constant and time t is in seconds. The initial velocity of the particle at t = 0 is v0 = 12 m/s and the particle reverses it direction of motion at t = 6 s. Determine the constant k and the displacement of the particle over the same 6-second interval of motion. Ans: k = 1/6 m/s4, Δs = 54 m

Answer 1

`X - Xo = 54m`

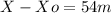
k = 1/18

Step-by-step explanation:

Data:

a = -k
`t^(2)`
`(m)/(s^(2) )`

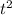
to = 0s Vo = 12m/s

t = 6s the particle chage it's moviment, so v = 0 m/s

We know that acceleration is the derivative of velocity related to time:

`a = (dV)/(dT)`

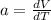
rearranging...

`a*dT = dV`

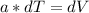
Then, we must integrate both sides:

`\int\limits^f_i {dV} \, dV =-k \int\limits^f_i {t^(2) } \, dT`

`V - Vo = -k(t^(3) )/(3)`

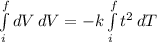
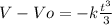
V = 0 because the exercise says that the car change it's direction:

`0 - 12 = -k(6^(3) )/(3)`

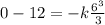
k = 1/6

In order to find X - Xo we must integer v*dT = dX

`V - Vo = -k(t^(3) )/(3)`

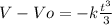
so...

`(Vo -k(t^(3) )/(3))dT = dX`

`\int\limits^f_i {dX} \, dX = \int\limits^f_i {Vo -k(t^(3) )/(3) } \, dT`

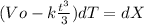
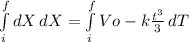
integrating...

`X - Xo = Vot -k(t^(4) )/(12)`

`X - Xo = 12*6 -(1)/(6)* (6^(4) )/(12)`

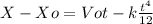
X - Xo = 54m