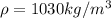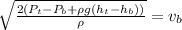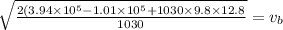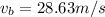Question

A sealed tank containing seawater to a height of 12.8 m also contains air above the water at a gauge pressure of 2.90 atm . Water flows out from the bottom through a small hole.

Answer 1

The velocity of water at the bottom,
`v_(b) = 28.63 m/s`

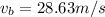
Given:

Height of water in the tank, h = 12.8 m

Gauge pressure of water,
`P_(gauge) = 2.90 atm`

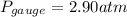
Solution:

Now,

Atmospheric pressue,
`P_(atm) = 1 atm = 1.01\tiems 10^(5) Pa`

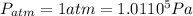
At the top, the absolute pressure,
`P_(t) = P_(gauge) + P_(atm) = 2.90 + 1 = 3.90 atm = 3.94* 10^(5) Pa`

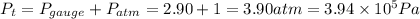
Now, the pressure at the bottom will be equal to the atmopheric pressure,
`P_(b) = 1 atm = 1.01* 10^(5) Pa`

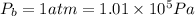
The velocity at the top,
`v_(top) = 0 m/s`, l;et the bottom velocity, be
`v_(b)`.

Now, by Bernoulli's eqn:

`P_(t) + (1)/(2)\rho v_(t)^(2) + \rho g h_(t) = P_(b) + (1)/(2)\rho v_(b)^(2) + \rho g h_(b)`

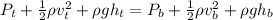
where

`h_(t) -  h_(b) = 12.8 m`

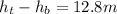
Density of sea water,
`\rho = 1030 kg/m^(3)`

`\sqrt{(2(P_(t) - P_(b) + \rho g(h_(t) - h_(b))))/(\rho)} =  v_(b)`

`\sqrt{(2(3.94* 10^(5) - 1.01* 10^(5) + 1030* 9.8* 12.8)/(1030)} =  v_(b)`

`v_(b) = 28.63 m/s`