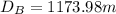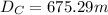Question

The route followed by a hiker consists of three displacement vectors A with arrow, B with arrow, and C with arrow. Vector A with arrow is along a measured trail and is 1550 m in a direction 25.0° north of east. Vector B with arrow is not along a measured trail, but the hiker uses a compass and knows that the direction is 41.0° east of south. Similarly, the direction of vector vector C is 20.0° north of west. The hiker ends up back where she started, so the resultant displacement is zero, or A with arrow + B with arrow + C with arrow = 0. Find the magnitudes of vector B with arrow and vector C with arrow.

Answer 1

`D_(B)=1173.98m\\D_(C)=675.29m`

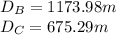
Step-by-step explanation:

If we express all of the cordinates in their rectangular form we get:

A = (1404.77 , 655.06) m

`B = A + ( -D_(B) *sin(41) , -D_(B) * cos(41) )`

`C = A + B + ( -D_(C) *cos(20) , D_(C) * sin(20) )`

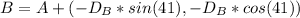
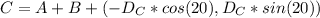
Since we need C to be (0,0) we stablish that:

`C = (0,0) = A + B + ( -D_(C) *cos(20) , D_(C) * sin(20) )`

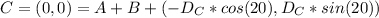
That way we make an equation system from both X and Y coordinates:

`A_(x) + B_(x) + C_(x) = 0`

`A_(y) + B_(y) + C_(y) = 0`

Replacing values:

`1404.77 - D_(B)*sin(41) - D_(C)*cos(20) = 0`

`655.06 - D_(B)*cos(41) + D_(C)*sin(20) = 0`

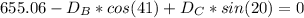
With this system we can solve for both Db and Dc and get the answers to the question:

`D_(B)=1173.98m`

`D_(C)=675.29m`