Answer:
(x+1) and (x-4)
Explanation:
Since, factors of an expression is the values which after multiplying together give the same expression.
Given quadratic equation,
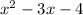
By the middle term splitting,

By distributive property,

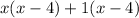
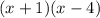
Since,
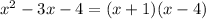
i.e. the factors of
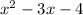 are (x+1) and (x-4).
are (x+1) and (x-4).