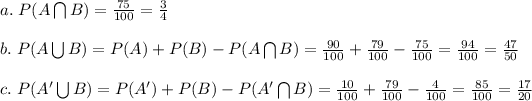Question

Samples of a cast aluminum part are classified on the basis of surface finish and edge finish. The results of 100 parts are summarized as follows. Edge finish Excellent Good Surface Excellent 75 4Finish Good 15 6Let A denote the event that a sample has excellent surface finish, and let B denote the event that a sample has excellent edge finish. If a part is selected at random, determine the following probabilities: (a) P(A B), (b) P(A U B) and (c) P(A' U B)

Answer 1

`a. \hspace{3} P(A\bigcap B) = (3)/(4)\\\\b. \hspace{3} P(A\bigcup B) = (47)/(50)\\\\c. \hspace{3} P(A'\bigcup B) = (17)/(20)\\\\`

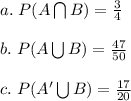
Explanation:

The information is configured in a double entry table in which the finishing information for the edge and surface is recorded, thus:

`\begin{array}{cccc}&E&B&Total\\E&75&4&79\\B&15&6&21\\&90&10&100\\\end{array}`

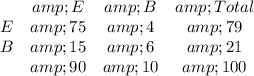
Let A denote the event that a sample has excellent surface finish, and let B denote the event that a sample has excellent edge finish.

`a. \hspace{3} P(A\bigcap B) = (75)/(100) = (3)/(4)\\\\b. \hspace{3} P(A\bigcup B) = P(A) + P(B) - P(A\bigcap B) = (90)/(100)+(79)/(100) - (75)/(100) = (94)/(100) =(47)/(50)\\\\c. \hspace{3} P(A'\bigcup B) = P(A') + P(B) - P(A'\bigcap B) = (10)/(100)+(79)/(100) - (4)/(100) = (85)/(100) =(17)/(20)\\\\`