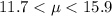Answer:
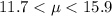
Explanation:
Given : Significance level :
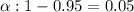
Sample size : n=45
Critical value :
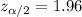
Sample mean :
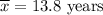
Standard deviation :
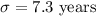
The confidence interval for population mean is given by :-
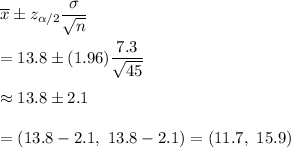
Hence, the 95% confidence interval estimate for the average number of years served by all Supreme Court justices is