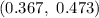Question

A survey of 85 families showed that 36 owned at least one DVD player. Find the 99% confidence interval estimate of the true proportion of families who own at least one DVD player. Place your limits, rounded to 3 decimal places, in the blanks. Place the lower limit in the first blank

Answer 1

Answer:
`(0.367,\ 0.473)`

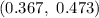
Explanation:

The confidence interval for population mean is given by :-

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

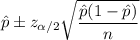
, where
`\hat{p}` is the sample proportion, n is the sample size ,
`z_(\alpha/2)` is the critical z-value.

Given : Significance level :
`\alpha:1-0.99=0.01`

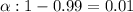
Sample size : n= 85

Critical value :
`z_(\alpha/2)=2.576`

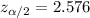
Sample proportion:
`\hat{p}=(36)/(85)\approx0.42`

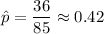
Now, the 99% confidence level will be :

`\hat{p}\pmz_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\\\\=0.42\pm(2.576)\sqrt{(0.42(1-0.42))/(85)}\\\\\approx0.42\pm0.053\\\\=(0.42-0.053,\ 0.42+0.053)=(0.367,\ 0.473)`

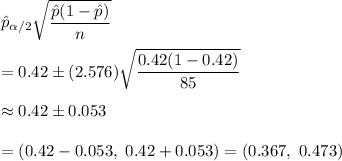
Hence, the 99% confidence interval estimate of the true proportion of families who own at least one DVD player is
`(0.367,\ 0.473)`