Question

Sketch these four lines y = 2x+1, y =-x, and x = 0 and x = 2. Then use integrals to find the area of the region bounded by these lines. Finally, check your answer by computing this area using simple geometry.

Answer 1

Area = 8

Explanation:

A skecth is given in the attached file, there are two extra lines used to calculate the area with simple geometry:

We must use a double integral to obtain the area:

`\int\limits^2_0 {\int\limits^b_a  \, dy } \, dx`

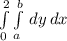
Where

b stands for y=2x+1

a stands for y=-x

Carring out the integrals we find the area:

`\int\limits^2_0 {(2x+1 - (-x))} \, dx =  \int\limits^2_0 {3x+1} \, dx = (3x^(2)/2+x) \left \{ {{2} \atop {0}} \right.\\ A =( 3*2^(2)/2) + 2 =8`

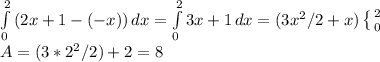
Geometrically we can divide the area bounded by this lines as two triangles and a rectangle from the figure and the intersection of these lines we kno that the three figures have a base of 2. The heigth of the rectangle is 1 and for the triangles we have 4 for the upper triangle and 2 for the lower.

Therefore:

`A = A_(upperT)+ A_(rect)+ A_(lowerT)`

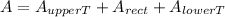
and

`A_(upperT)=2*4/2=4\\A_(rect)=2*1=2\\ A_(lowerT)=2*2/2=2`

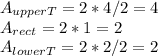
Summing the four areas we have:

A=8

Greeting!