Question

Between which two integers can the square root of 15 be found?

Answer 1

`3<√(15)<4`

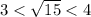
Explanation:

We are asked to find the integers such that square root of 15 lies between them.

We know that perfect square less than 15 is 9 and perfect square greater than 15 is 16.

We can represent this information in an inequality as:

`√(9)<√(15)<√(16)`

`√(3^2)<√(15)<√(4^2)`

`3<√(15)<4`

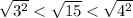
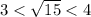
Therefore, the square root of 15 lies 3 and 4.

Answer 2

3 and 4

Explanation:

Consider squares on either side of 15, that is 9 and 16, so

`√(9)` <
`√(15)` <
`√(16)`, that is

3 <
`√(15)` < 4