Question

What is the least amount of energy that can be emitted by an excited electron in a hydrogen atom falling from an excited state directly to the n = 3 state? What is the quantum number n for the excited state? Humans cannot visually observe the photons emitted in this process. Why not?

Answer 1

1.
`E=1.059x10^(-19)J`

2.
`n=4`

3. The associated wavelength belongs to the infrared spectrum which is invisible for humans.

Step-by-step explanation:

Hello,

1. At first, according to the equation:

`E=E_oZ^2((1)/(n_1^2)-(1)/(n_2^2))`

Whereas
`E` is the emitted energy,
`E_o` the first level energy,
`Z` the atomic number,
`n_1` the first level and
`n_2` the second level. In such a way, the closest the
`n`'s are, the least the amount of emitted energy, therefore,
`n_1=3` (based on the statement) and
`n_2=4`, thus, the least amount of energy turns out being:

`E=(2.179x10^(-18)J)(1^2)((1)/(3^2)-(1)/(4^2))\\E=1.059x10^(-19)J`

2. Secondly, and based on the first question, the quantum number for the excited state is mandatorily
`n=4`

3. Finally, to substantiate why we cannot observe the emitted photons we apply the following equation:

`E=(hc)/(\lambda) \\\lambda=(hc)/(E)=((6.62607004x10^(-34) m^2 kg / s)(299 792 458m/s))/(1.059x10^(-19)m^2 kg / s^2)  \\\lambda=1.88x10^(-6)m`

Whereas the obtained wavelength corresponds to the infrared spectrum which is not observable by humans.

Best regards.

Answer 2

The least amount of energy emitted in this case is 0.6 eV.

The corresponding quantum number n would be n=4.

The wavelenght asociated to the emitted photon would be 2.06
`\mu`m, corresponding to the Infrared spectrum.

Step-by-step explanation:

For calculating the energy of an electron emitted/absorbed in an electronic transition of the hydrogen atom, the next equation from the Bohr model can be used:

`E=E_(0) Z^2 [(1)/(n_1^2)-(1)/(n_2^2)]`

, where E is the photon energy,
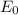`E_0` is the energy of the first energy level (-13.6 eV), Z is the atomic number,
`n_1` is the quantum number n of the starting level and
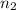`n_2` the quantum number n of the finishing level. In this case,
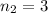`n_2=3`, and
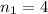`n_1=4`, because this excited level is the next in energy to n=3.

Considering that
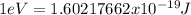`1 eV= 1.60217662x10^(-19) J`, and using the Planck equation
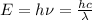`E=h\\u=(hc)/(\lambda)`, you can calculate the wavelenght or the frequency associated to that photon. Values in the order of
`\mu`m in wavelenght belong to the Infrared spectrum, wich can not being seen by humans.