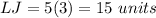Question

Triangle J K L is shown. Angle J K L is a right angle. An altitude is drawn from point K to point M on side L J to form a right angle. The length of K M is 6 and the length of M J is 3. What is the length of line segment LJ? 9 units 12 units 15 units 18 units

Answer 1

The answer would be option C. 15 units :)

Explanation:

Did it on edge :D

Hope this helps!

Answer 2

`LJ=15\ units`

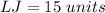
Explanation:

see the attached figure to better understand the problem

step 1

Find the length side KJ

In the right triangle JKM

Applying the Pythagoras Theorem

`KJ^(2)=JM^(2)+KM^(2)`

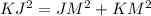
we have

`JM=3\ units`

`KM=6\ units`

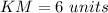
substitute

`KJ^(2)=3^(2)+6^(2)`

`KJ^(2)=45}`

`KJ=√(45)\ units`

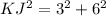
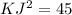
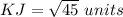
simplify

`KJ=3√(5)\ units`

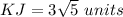
step 2

Find the value of cosine of angle MJK in the right triangle JKM

`cos(JKM)=JM/KJ`

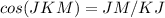
substitute the values

`cos(JKM)=(3)/(3√(5))`

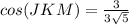
simplify

`cos(JKM)=(√(5))/(5)` -----> equation A

step 3

Find the value of cosine of angle MJK in the right triangle JKL

`cos(JKM)=KJ/LJ`

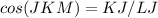
we have

`KJ=3√(5)\ units`

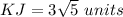
`cos(JKM)=(√(5))/(5)` ----> remember equation A

substitute the values

`(√(5))/(5)=(3√(5))/(LJ)`

Simplify

`LJ=5(3)=15\ units`