Answer: The molar mass of the unknown compound is 152 g/mol.
Step-by-step explanation:
Depression in freezing point is given by:
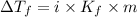
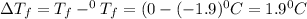 = Depression in freezing point
= Depression in freezing point
i= vant hoff factor = 1 (for non electrolyte)
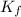 = freezing point constant =
= freezing point constant =
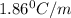
m= molality

Weight of solvent (water)= 106.0 g = 0.106 kg
Molar mass of unknown non electrolyte = M g/mol
Mass of unknown non electrolyte added = 16.5 g
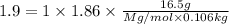

Thus the molar mass of the unknown compound is 152 g/mol.