Question

The Stokes-Oseen formula for drag force, F, on a sphere of diameter D in a fluid stream of low velocity, v, density rho and viscosity µ is
`F = 3\pi \mu DV + (9\pi)/(16) \rho V^2 D^2`Is this formula dimensionally consistent?

Answer 1

the equation is dimensionally consistent

Step-by-step explanation:

To verify that the formula is dimensionally consistent, we must verify the two terms of the sum and verify that they are units of force. We achieve this by putting the units of each dimensional term of the equation and verifying that the answer is in units of force

μ=viscosity=Ns/m^2

D=diameter

V=velocity

ρ=density=Kg/m^3π

First term

3πμDV=
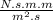`(N.s.m.m)/(m^(2).s )`=N

the first term is dimensionally consistent

second term

(9π/16)ρV^2D^2=
`(kg.m^2.m^2)/(m^3.s^2) =(kg.m)/(s^2) =N`

.

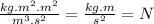
as the two terms are in Newtons it means that the equation is dimensionally consistent