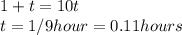Question

Achilles and the tortoise are having a race. The tortoise can run 1 mile (or whatever the Hellenic equivalent of this would be) per hour. Achilles runs ten times as fast as the tortoise so the tortoise gets a head start of 1 mile. The race begins! By the time Achilles reaches the 1 mile mark, the tortoise is .1 miles ahead. By the time Achilles runs this extra tenth of a mile, the tortoise is still .01 miles ahead. This process continues; each time Achilles reaches the point where the tortoise was, the tortoise has moved ahead 1/10 as far. Can Achilles ever catch the tortoise? If so, when? If not, who would you bet on?

Answer 1

Surely Achilles will catch the Tortoise, in 400 seconds

Step-by-step explanation:

The problem itself reduces the interval of time many times, almost reaching zero. However, if we assume the interval constant, then it is clear that in two hours Achilles already has surpassed the Tortoise (20 miles while the Tortoise only 3).

To calculate the time, we use kinematic expression for constant speed:

`x_(final)=x_(initial)+t_(tor)v_(tor)=1+t_(tor)\\x_(final)=x_(initial)+t_(ach)v_(ach)=10t_(ach)`

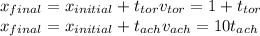
The moment that Achilles catch the tortoise is found by setting the same final position for both (and same time as well, since both start at the same time):

`1+t=10t\\t=1/9 hour=0.11 hours`