Question

All the fourth-graders in a certain elementary school took a standardized test. A total of 81% of the students were found to be proficient in reading, 74% were found to be proficient in mathematics, and 64% were found to be proficient in both reading and mathematics. A student is chosen at random.(a) What is the probability that student is proficient in mathematics but not in reading?(b) What is the probability that student is proficient in reading but not in mathematics?

Answer 1

The probability that a student is proficient in mathematics, but not in reading is, 0.10.

The probability that a student is proficient in reading, but not in mathematics is, 0.17

Explanation:

Let's define the events:

L: The student is proficient in reading

M: The student is proficient in math

The probabilities are given by:

`P (L) = 0.81\\P (M) = 0.74\\P (L\bigcap M) = 0.64`

`P (M\bigcap L^c) = P (M) - P (M\bigcap L) = 0.74 - 0.64 = 0.1\\P (M^c\bigcap L) = P (L) - P (M\bigcap L) = 0.81 - 0.64 = 0.17`

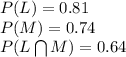
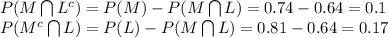
The probability that a student is proficient in mathematics, but not in reading is, 0.10.

The probability that a student is proficient in reading, but not in mathematics is, 0.17