Answer:
The angle is
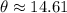 degrees.
degrees.
Step-by-step explanation:
Se the attached drawing if you need a visual aid for the explanation. Let
 be the angle of elevation of the plante which in itself is the same drop angle that the pilot measures. Let
be the angle of elevation of the plante which in itself is the same drop angle that the pilot measures. Let
 be the horizontal distance from the target and
be the horizontal distance from the target and
 the height of the plane. We know that the package is dropped without any initial vertical speed, that means that it has a y-position equation of the form:
the height of the plane. We know that the package is dropped without any initial vertical speed, that means that it has a y-position equation of the form:
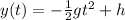
If we set
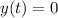 we are setting the condition that the package is in the ground. We can then solve for t and get the flight time of the package.
we are setting the condition that the package is in the ground. We can then solve for t and get the flight time of the package.
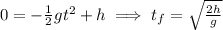 .
.
If the flight time is -
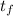 then the distance b can be found in meters by taking into account that the horizontal speed of the plane is
then the distance b can be found in meters by taking into account that the horizontal speed of the plane is
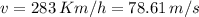 .
.
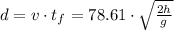
The angle is thus
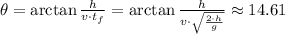 degrees.
degrees.