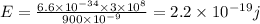Question

Consider light of wavelengths 400 nm (UV), 550 nm (green, visible), and 900 nm (infrared). What is the energy associated with a 400 nm (UV) photon, a 550 nm (green, visible) photon, and a 900 nm (infrared) photon?

Answer 1

Energy of UV light
`=4.95* 10^(-19)j`

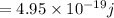
Energy of green light
`=3.6* 10^(-19)j`

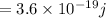
Energy of infrared light
`=2.2* 10^(-19)j`

Step-by-step explanation:

We have given the wavelength of UV light = 400 nm
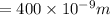`=400* 10^(-9)m` , wavelength of green light = 550 nm and wavelength of infrared = 900 nm

Speed of light
`c=3* 10^8m/sec`

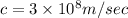
Plank's constant
`h=6.6* 10^(-34)`

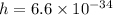
Energy of the signal is given by
`E=h\\u =h(c)/(\lambda )`

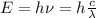
So energy of UV light
`E=(6.6* 10^(-34)*3* 10^8)/(400* 10^(-9))=4.95* 10^(-19)j`

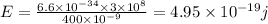
Energy of green light
`E=(6.6* 10^(-34)*3* 10^8)/(550* 10^(-9))=3.6* 10^(-19)j`

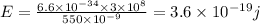
Energy of infrared light
`E=(6.6* 10^(-34)*3* 10^8)/(900* 10^(-9))=2.2* 10^(-19)j`