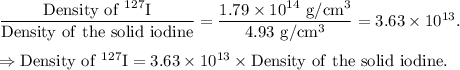Answer:
Density of 127 I =
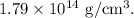
Also,

Step-by-step explanation:
Given, the radius of a nucleus is given as
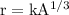 .
.
where,
- A is the mass number of the nucleus.
The density of the nucleus is defined as the mass of the nucleus M per unit volume V.

For the nucleus 127 I,
Mass, M =
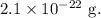
Mass number, A = 127.
Therefore, the density of the 127 I nucleus is given by
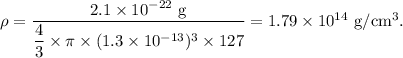
On comparing with the density of the solid iodine,