Question

Given that y is directly proportional to x^2 and that y=2 when x=3 find the value of y when x=6

​

Answer 1

Answer:y=4/3

y is directly proportional to x^2 is written as

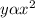`y \alpha {x}^(2)` introducing a constant,

y=kx^2

but from the question, when y=2 , x=3 . putting it in the formula to get the value of k

`2 = {3}^(2) * k`

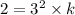
2=9k . dividing through by 9 to get the value of k

`(2)/(9) = (9k)/(9)`

`k = (2)/(9)`

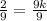
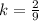
putting it in the general expression

`y = (2)/(9) x`

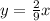
the value of y when x=6

`y = (2)/(9) * 6`

`y = (4)/(3)`

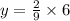
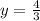
therefore the value of y when x=6 is

4/3